om parhad

K-Nearest Neighbors (KNN) is a simple yet effective machine-learning algorithm that classifies a data point based on the majority label of its k nearest neighbors. However, the choice of k directly influences how well the model balances bias and variance.

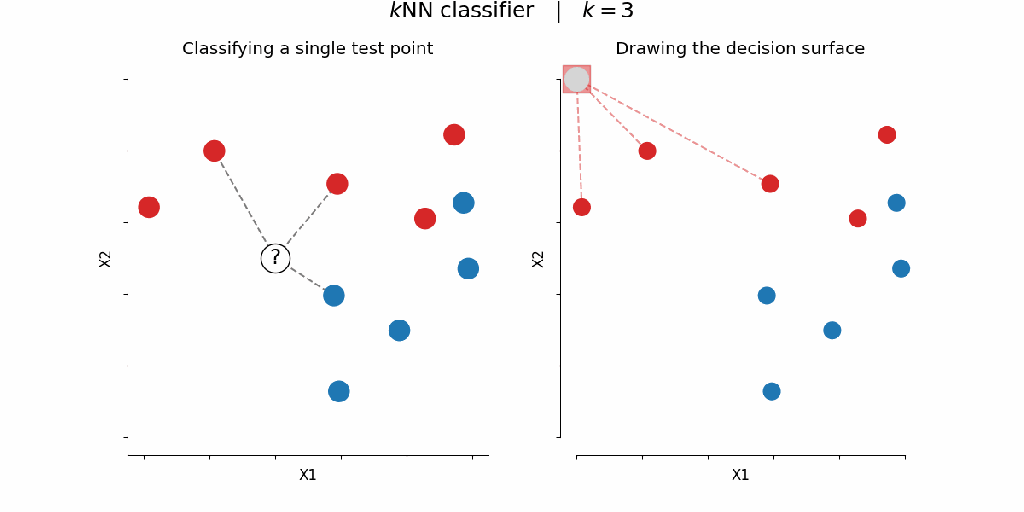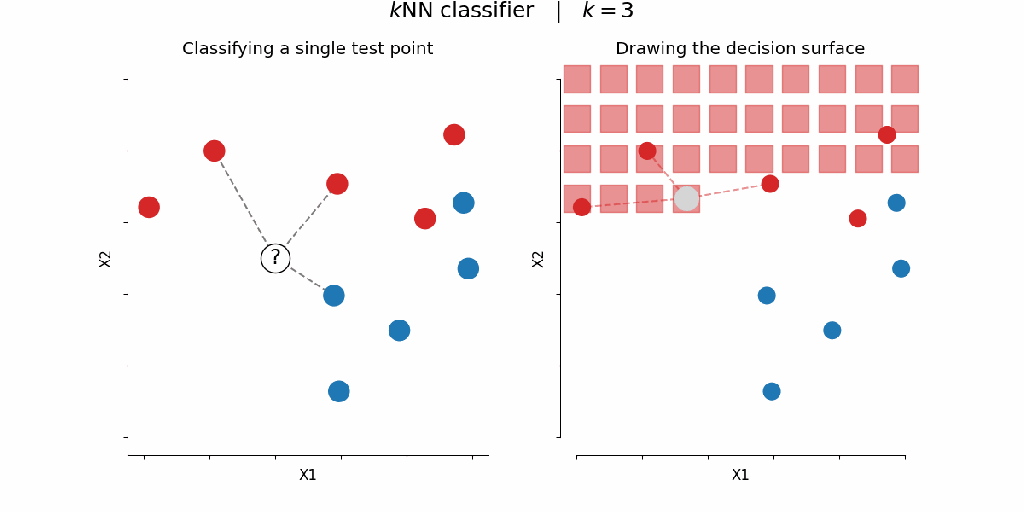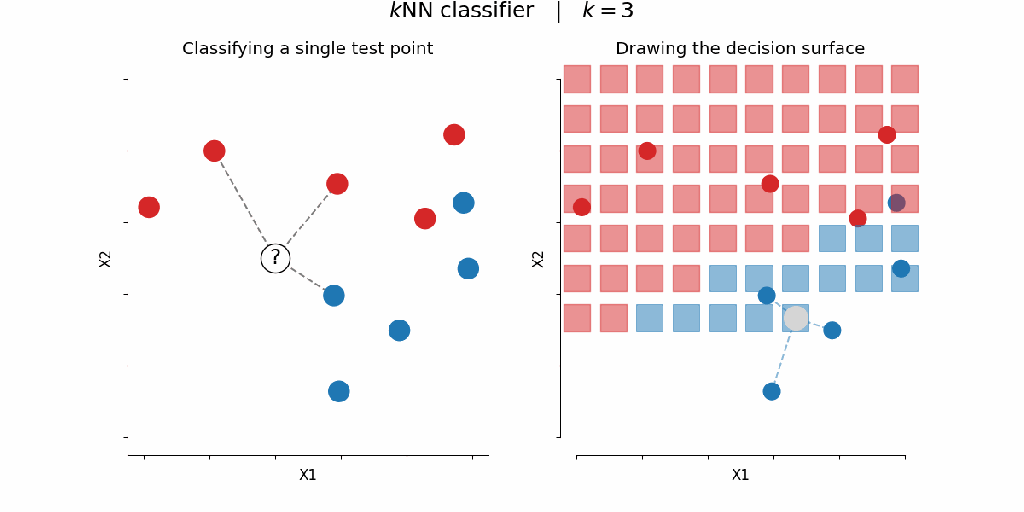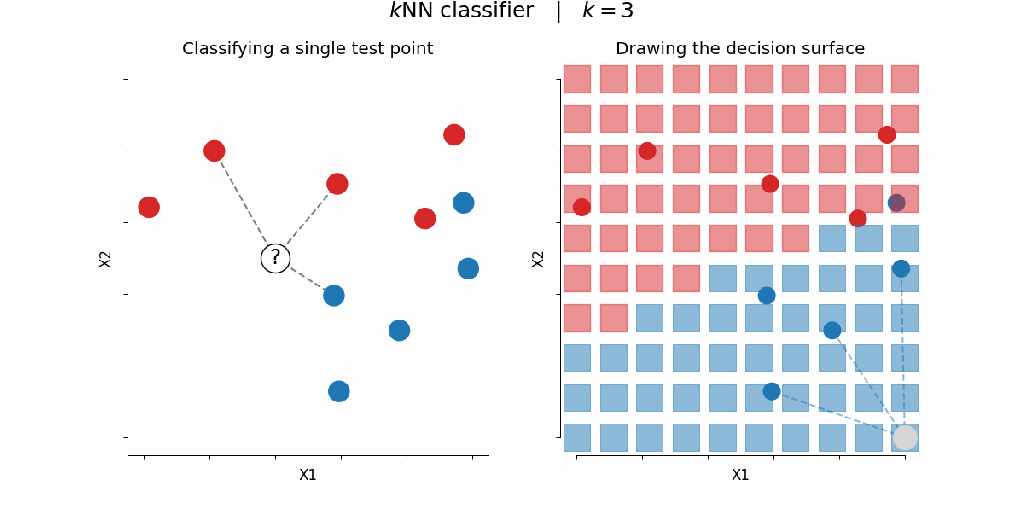
Dataset Used: Iris Dataset (contains 150 samples across 3 flower species — Setosa, Versicolor, and Virginica)
Features: Sepal length, Sepal width, Petal length, Petal width
Distance Metric: Euclidean Distance
Validation Technique: 10-Fold Cross-Validation
Software: Weka

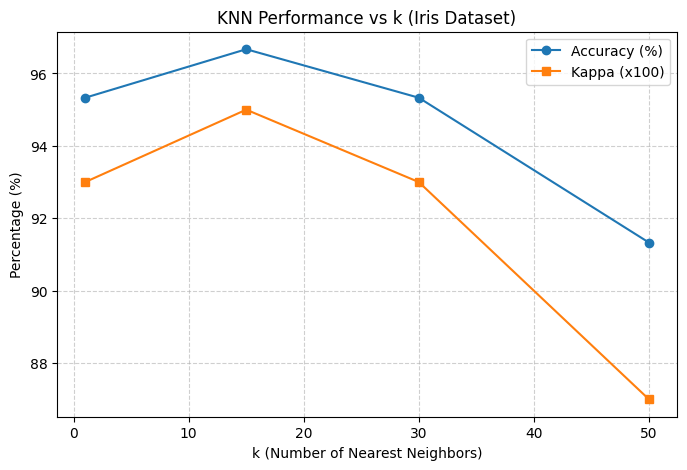
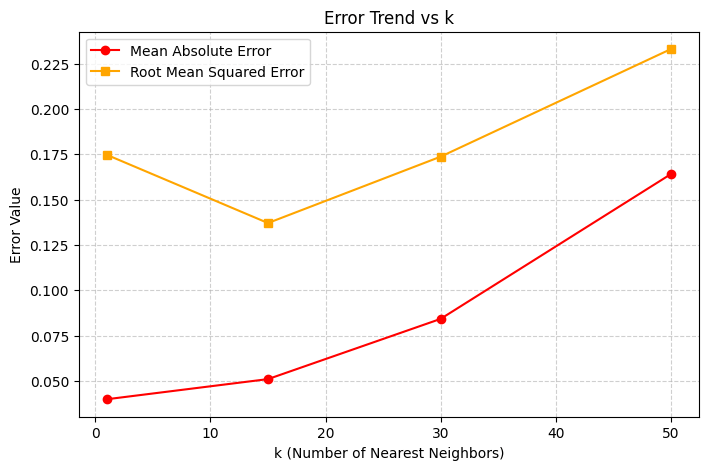
k	Accuracy (%)	Kappa	MAE	RMSE
1	95.33	0.93	0.0399	0.1747
15	96.67	0.95	0.0510	0.1371
30	95.33	0.93	0.0842	0.1737
50	91.33	0.87	0.1640	0.2330

Accuracy: Percentage of correctly classified samples.

Cohen’s Kappa: Measures agreement between predicted and actual labels, adjusting for chance.

MAE (Mean Absolute Error): Measures average magnitude of classification error.

RMSE (Root Mean Squared Error): Penalizes large misclassifications more heavily.

Visualization:

Interpretation:

• Accuracy and Kappa improve up to k = 15, then drop after that.
• MAE and RMSE are lowest at k = 15, confirming it’s the most balanced choice.

My Conclusion

When k is too small, the algorithm reacts to noise, causing overfitting.
When k is too large, it smooths over important local patterns, leading to underfitting.
An intermediate k = 15 offers the best trade-off between these two extremes.